(1.1)
La masse des neutrinos est-elle conciliable avec la violation de la parité dans l'interaction faible?
La masse des neutrinos est-elle conciliable avec la violation de la parité dans l'interaction faible?
Yves SAGNIER
Dans de nombreux ouvrages de vulgarisation scientifiques concernant la physique des particules, on décrit les neutrinos comme des particules "gauches" (voir plus loin à la section hélicité ce que recouvre ce terme), de masse nulle ou "presque" nulle. C'est à escient que deux termes ont été placés entre guillemets dans la phrase précédente. En effet, il est généralement indiqué dans ces ouvrages que :
1) le fait que les neutrinos soient toujours gauches explique le phénomène de violation de la parité dans l'interaction faible (voir plus loin);
2) le fait que la masse puisse être presque nulle, c'est à dire surtout NON nulle permettrait, grâce au nombre gigantesque de neutrinos fourmillant dans l'univers, d'en retrouver ce qu'on appelle la "masse manquante" qui, ajoutée à celle qu'on a déjà identifiée, assurerait à l'univers l'équilibre entre les modèles cosmologiques de contraction future ou d'expansion perpétuelle.
Le problème, c'est que si l'on regarde de plus près, ces deux assertions sont contradictoires. Je ne pense pas que cela ait échappé aux nombreux scientifiques travaillant dans le domaine, mais cela n'empêche pas que la violation de la parité est une propriété intangible depuis 1957, et que depuis plus longtemps encore on recherche l'éventuelle masse des neutrinos (on continue encore de nos jours).
N'étant pas moi-même directement dans le milieu concerné, cette contradiction sous-jacente - et pourtant jamais formulée ni par conséquent expliquée - dans tous les ouvrages "grand public" que j'ai pu lire m'a donné envie d'en savoir plus, et c'est pourquoi j'ai écrit cette note qui, je l'espère, résume à peu près tout ce que l'on sait sur les deux termes de l'alternative.
C'est Wolfgang Pauli, célèbre physicien, qui, en 1931, suggéra l'existence de cette particule, afin d'expliquer où était dissipée une partie de l'énergie issue du phénomène de radioactivité β.
La dénomination β vient de ce que ce phénomène est d'abord apparu comme l'un des 3 rayonnements radioactifs identifiés par Becquerel. Ces rayonnements furent appelés par les trois premières lettres grecques α, β et γ. Ce n'est que plus tard que l'on trouva leur contenu réel de ces rayonnements, d'ailleurs fort différents :
|
α |
noyaux d'hélium |
|
β |
électrons [1] |
| γ | photons |
Ce qui précède est leur constitution particulaire. En fait, spécialement pour le dernier, on met plus facilement en évidence sa composante ondulatoire (rayonnement électromagnétique), mais les deux aspects ne sont pas contradictoires.
En particulier, la radioactivité β a été rattachée à l'interaction nucléaire faible [2] et consiste dans son expression la plus simple en une expulsion d'électrons par un noyau atomique, ce qui peut être codifié par la réaction suivante :
(1.1)
Dans ce cas, l'élément X a augmenté son numéro atomique et s'est transmuté en Y, qui est le suivant dans la classification périodique tout en gardant le même nombre de masse A. Cela signifie qu'au niveau nucléaire a eu lieu la réaction suivante :
(1.2)
Un neutron s'est "transformé" en une paire proton-électron. En fait, aussi bien la réaction 1.1 que la 1.2 sont incomplètes et insatisfaisantes, du point de vue bilan énergétique. Si l'on considère par exemple la réaction suivante :
(1.3)
Dès 1919, James Chadwick [3] a dressé la courbe de distribution d'énergie apparemment dégagée par la réaction 1.3 à partir de mesures effectuées sur les électrons générés au cours de cette réaction (sur un grand nombre d'atomes, c'est à dire de réactions élémentaires). Il avait dessiné une courbe portant en abscisse une grandeur d'impulsion p (équivalent à une quantité de mouvement) et en ordonnée le pourcentage d'électrons détectés dans une certaine tranche autour de cette impulsion.
Cette courbe - qui est en fait un histogramme lissé - avait à peu près l'allure suivante [Ref. 1, p.159]:
Figure 2.1 Spectre d'impulsion du rayonnement Béta
Cette courbe signifie que les électrons détectés peuvent avoir une impulsion (et donc une énergie) très variable, mais inférieure à un certain maximum (la partie finale de la courbe vers les 3000) qu'on peut appeler Pmax (ou Emax). Par ailleurs, les électrons se répartissent de manière préférentielle autour de la moyenne. Sur la courbe, il est malaisé de lire la valeur max, mais par extrapolation sur une autre courbe, on peut la déterminer précisément.
Avant d'aller plus loin, on peut se demander d'où provient l'énergie (ou l'impulsion) des électrons. On sait que l'énergie se conserve sous une forme ou une autre (énergie cinétique, énergie potentielle, masse...) et que les électrons doivent bien avoir emprunté quelque part, et leur masse et leur impulsion. Quand un neutron se transforme en proton, il perd bien un peu de masse, mais ce n'est même pas suffisant pour la seule masse de l'électron!
En fait, la réaction 1.3 dégage beaucoup d'énergie du fait que l'énergie de cohésion (ou de liaison) de l'atome de Césium est supérieure à celle de l'atome de Baryum. L'énergie de cohésion est une partie de la masse du noyau convertie pour maintenir les nucléons (composants du noyau, c'est à dire neutrons et protons) ensemble alors que leur tendance naturelle serait au contraire de s'écarter les uns des autres, spécialement les protons dont les charges toutes positives se repoussent. La force attractive inverse qui utilise l'énergie de cohésion est la force (ou interaction) forte [4] .
Quand on fait le calcul, on s'aperçoit que la différence des énergies de cohésion Césium - Baryum correspond à la valeur maximum Emax des électrons. Ce fait n'est pas surprenant : il faut bien que l'énergie dissipée se retrouve quelque part (principe de conservation) et Emax ne pouvait pas être supérieur à cette différence d'énergies (sinon, la question n'était plus "où part l'énergie?» mais "d'où vient-elle?"). Ce qui l'est beaucoup plus, c'est que l'énergie des électrons n'est pas TOUJOURS égale à ce maximum (on voit bien sur la courbe que ça n'arrive d'ailleurs pratiquement jamais) et qu'elle est généralement plutôt proche de la moitié. Il s'ensuit que dans la réaction 1.3, une partie de l'énergie produite par la transmutation Césium -> Baryum ne se retrouve pas dans l'impulsion de l'électron. Alors, où va-t-elle?
Voilà qui explique la phrase que l'on trouve dans beaucoup de livres (souvent sans autre explication) :
« Le spectre continu de la répartition des impulsions des électrons produits par la radioactivité est en contradiction avec la loi de conservation de l'énergie. »
L'explication fournie par Pauli en 1931 fut donc de
postuler l'existence
d'une nouvelle particule "voleuse" (d'énergie),
électriquement
neutre, de masse infime et pratiquement pas détectable. Celle-ci
serait
produite dans la réaction 1.3 et s'emparerait du reste de
l'énergie
(c'est à dire
Emax-Eélectron)
mais ne serait pas détectée. Plus tard, dans sa
théorie
explicative de l'interaction faible, Fermi introduisit une telle
particule
qu'il baptisa "neutrino" (petit neutre). En fait, dans la
radioactivité
β , ce sont des
antineutrinos [5]
(notés
)
qui
apparaissent, ce qui permet de compléter la réaction 1.2
comme
suit :
(1.4)
Mais neutrinos comme antineutrinos sont particulièrement difficiles à détecter, et ce ne fut qu'en 1956 que Frederik Reines et Clyde Cowan réussirent à mettre en évidence des antineutrinos émis par une pile atomique à Savannah, Géorgie (États-Unis) [Ref. 2]. En fait cette "mise en évidence" a été réalisée de manière indirecte, grâce à l'observation de la réaction suivante où sont capturés des antineutrinos et où sont produits des positrons [6] :
(1.5)
Il est intéressant de noter que l'on a postulé que la réaction 1.3 s'accompagnait de la production d'une particule "invisible" et que l'on assure avoir prouvé son existence en observant une autre réaction (l'inverse pourrait-on dire) mais toujours sans avoir vu la particule en question. En fait, ce n'est pas aussi arbitraire que cela en a l'air : il a fallu rapprocher - géographiquement - la deuxième réaction de la première pour qu'elle puisse avoir lieu (et surtout être observée), preuve que la particule fantôme postulée par la théorie devait bien exister et être passée de l'une à l'autre en grandes quantités [7] .
Neutrinos et antineutrinos ont a priori les mêmes caractéristiques (observables), sauf leur hélicité qui est opposée. Pour comprendre cette propriété, nous allons d'abord faire un rappel sur l'orientation de l'espace.
On sait que tout point d'un espace à 3 dimensions est repéré de manière unique et non ambiguë par 3 coordonnées x, y et z, rapportées à un référentiel défini par 3 axes orientés (de manière à définir les valeurs négatives et positives) orthogonaux deux à deux et se croisant en un même point origine, comme indiqué sur le schéma ci-dessous :
Figure 3.1 : repère Oxyz
Sur le schéma, les axes Ox et Oz sont dans le plan de la page tandis qu'Oy (vu en perspective) "fuit" vers l'arrière de la page. La vue en perspective montre des angles déformés xOy et yOz (censés être à 90 degrés) tandis qu'xOz est conforme. Il est important de remarquer que par ce simple schéma, nous avons choisi une origine arbitraire, puis un axe arbitraire (disons Ox), ensuite un axe choisi arbitrairement dans un plan orthogonal (Oy), et qu'Oz s'en est automatiquement déduit, à un choix près : celui du sens. On aurait pu choisir d'orienter Oz vers le bas plutôt que vers le haut. Pour Ox, puis Oy, on avait également le choix entre deux sens, mais cela n'aurait pas porté à conséquence : en effectuant des rotations et/ou des translations, on se serait ramené à une situation identique face au choix d'Oz. Finalement, faire le choix d'orienter Oz vers le haut ou vers le bas en finale revient à orienter tout l'espace.
Quels que soient les choix faits pour l'origine et les axes orientés Ox, Oy et Oz, on ne peut tomber que sur deux cas différents qui sont :
Figure 3.2 : les 2 orientations de l'espace
Il est important de se rendre compte que tout choix de 3 axes orthogonaux retombe sur l'un des deux cas ci-dessus, moyennant une translation et une rotation (on dit alors qu'ils sont superposables). Ces deux opérations, translation et rotation, ne modifient pas l'orientation de l'espace, ni de tout objet qui s'y trouve. Dans la vie courante, ce sont des actions qu'on effectue à tout instant sur tous les objets possibles, et ceci ne modifie en rien ces objets.
Pour passer du cas N°1 au cas N°2, il faut appliquer une autre transformation, qui est une symétrie-plan (ou symétrie-miroir). Il est évident que l'image du repère N°1 par une symétrie par rapport au plan xOy horizontal donne le repère N°2. Mais en fait, c'est le cas pour toute symétrie-plan, quel que soit le plan retenu (il suffit ensuite d'effectuer une translation et une rotation). La symétrie plan modifie donc l'orientation de l'espace : en effet, c'est une opération qu'on n'effectue pas avec les objets courants (sauf exceptions rares, et encore s'agit-il d'approximations, comme par exemple un gant que l'on retourne), et la seule véritable approche qu'on en a est de regarder le monde inversé tel qu'il apparaît dans un miroir (mais c'est là un monde virtuel).
Et pourtant, l'orientation de l'espace est un choix complètement arbitraire fait a priori. Il découle totalement des notions de droite et de gauche, qui ont été inventées par l'espèce humaine pour... s'orienter. Et cela a été nécessaire parce que le monde (au moins macroscopique) recèle des asymétries qui à leur tour permettent d'orienter l'espace. Si ce n'était pas le cas, la droite et la gauche n'auraient aucun sens concret, et ne pourraient même pas être communiquées d'une personne à l'autre.
Par convention, on définit une orientation privilégiée en choisissant le repère N°1 ou tout autre repère qui lui est superposable). Il est dit être direct ou droit. Par opposition, le repère N°2 (ou tout autre repère superposable) est dit indirect ou gauche. Pour se rendre compte à quel point ces définitions sont liées aux notions de droite et de gauche, il suffit de voir qu'un repère direct est caractérisé par le fait que si l'on se place debout suivant l'axe Oz et qu'on regarde en direction de l'axe Oy, l'axe Ox est à droite, tandis que pour le repère indirect, il serait alors à gauche.
L'hélicité est une propriété des systèmes en rotation. Elle est liée à la manière d'orienter l'espace. Elle consiste à identifier la manière dont le système tourne par rapport à l'orientation de son axe. En particulier, elle permet de communiquer simplement le sens de cette rotation. Considérons par exemple une sphère qui tourne autour d'un axe vertical z'z :
Figure 4.1 : sphère en rotation
Sans autre renseignement, il demeure une ambiguïté sur le sens de la rotation : si l'on prend un point sur l'équateur de la sphère, de notre côté de la page, en un temps infinitésimal δt ce point se sera déplacé soit vers la droite soit vers la gauche. Il n'y a que ces deux possibilités :
Figure 4.2 : rotations droite et gauche
On dit que la première rotation est "droite" et la seconde "gauche". Cette propriété est relative à l'orientation de l'axe z'z. Si l'on inverse le sens de cet axe, une rotation droite devient gauche et inversement, car la définition initiale est dépendante de cet axe :
<<Une rotation par rapport à un axe orienté z'z est dite droite si, quand cet axe est vertical et orienté vers le haut, le déplacement infinitésimal [8] d'un point situé entre cet axe et l'observateur s'effectue vers la droite.>>
En particulier, une rotation droite de 90° ayant pour axe orienté Oz transforme l'axe Ox en l'axe Oy (en gardant l'orientation positive de ceux-ci), si le repère Oxyz est direct.
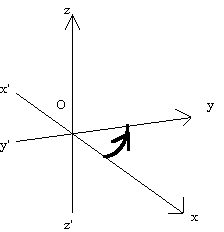
Figure 4.3 : une rotation droite de 90° fait passer de Ox à Oy
Notons que cette propriété de rotation est dépendante des définitions de droite et de gauche, encore une fois. Par exemple, si l'on effectue un changement de sens de l'axe z'z, cela revient à faire une symétrie-plan par rapport à un miroir horizontal, ce qui inverse bien la droite et la gauche.
Par ailleurs, il est évident que les deux schémas de la figure 4.2 sont images l'un de l'autre par une symétrie-miroir verticale, mais aussi horizontale :
Figure 4.4 : effet des réflexions-miroir sur le sens des rotations
Les schémas précédents s'appliquent à des corps en rotation par rapport à un axe. Quand le corps se déplace le long de cet axe, on peut alors lui définir une hélicité : on dit que le corps est d'hélicité droite ou positive s'il est animé d'un mouvement de rotation droit par rapport à l'axe de son déplacement orienté par le sens de son vecteur vitesse. Dans le cas contraire, il est d'hélicité gauche ou négative. Enfin, l'hélicité est dite égale à zéro si le corps n'est pas du tout animé d'un mouvement de rotation par rapport à son axe de déplacement.
Par exemple, dans la figure ci-dessous, les sphères se déplaçant vers le haut, on définit leur hélicité respective comme suit :
Figure 4.5 : hélicités droite et gauche
Pourquoi parle-t-on d'hélicité? Parce qu'un point placé sur un objet d'hélicité non nulle décrit une spirale - ou hélice - dans l'espace. Et l'hélice est bien sûr droite ou gauche selon que l'hélicité est elle-même droite ou gauche.
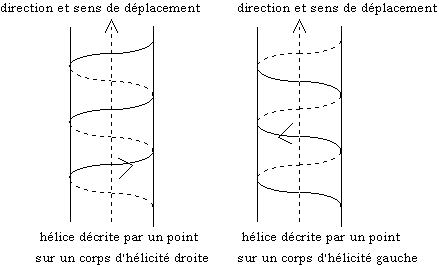
Figure 4.6 : hélices droite et gauche
Sur la figure 4.6, on a rajouté les cylindres sur lesquels s'inscrivent les hélices formées par les points en rotation.
Pour fixer les idées, un tire-bouchon est généralement d'hélicité droite : pour le faire rentrer dans le bouchon et donc le faire avancer suivant l'axe de la bouteille, il faut faire tourner sa partie la plus haute de gauche à droite (et c'est pareil pour les robinets) :
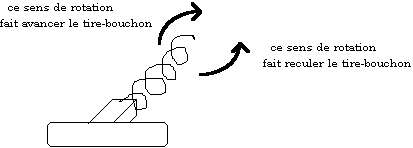
Figure 4.7 : exemple du tire-bouchon d'hélicité droite
Il existe un moyen
mathématique de
quantifier l'hélicité d'un corps, par le biais de ses 2
vecteurs
de vitesse et de rotation. Le vecteur rotation,
généralement
noté
,
a pour module
ω (vitesse angulaire) et est dirigé
suivant
l'axe de rotation, de manière que la rotation soit droite par
rapport
à lui, comme indiqué sur les exemples ci-dessous :
Figure 4.8 : vecteurs rotation
Dès lors,
l'hélicité
d'un corps est positive ou droite si et seulement si son vecteur
est dans le
même
sens que son vecteur vitesse
,
c'est à
dire que le produit scalaire
est
positif.
Dans le cas contraire, l'hélicité est gauche.
Figure 4.9 : vecteurs rotation et vitesse
Si l'on se réfère à ce qui précède, l'hélicité d'une particule devrait être liée à son sens de rotation propre par rapport à son sens de déplacement sur sa trajectoire... Oui, mais une particule tourne-t-elle vraiment sur elle-même? On sait que l'on peut leur attribuer un vecteur vitesse à défaut de trajectoire (car les particules, objets quantiques, ne se déplacent pas de manière continue. Elles sont quelque part à un instant donné, puis ailleurs quand on les regarde à nouveau, mais qu'ont-elles fait entre-temps ... Existaient-elles seulement?), mais en la mesure où on doute de plus en plus de pouvoir leur assigner un volume et où les considérer comme ponctuelles ne change rien à leurs propriétés, que signifie "tourner sur elles-mêmes"?
Il faut faire fi de son intuition liée aux phénomènes et aux objets macroscopiques et se contenter de ce qu'on peut mesurer. Or, justement, il y a un nombre quantique attribué aux particules qui joue assez bien le rôle d'une mesure de rotation propre, c'est le spin. Celui-ci décrit un certain état d'orientation de la particule, et se manifeste dans certaines interactions comme l'équivalent d'un moment cinétique propre, par exemple des expériences où intervient le moment magnétique qui est proportionnel au spin, comme dans la physique classique.
Dans le cas général, un moment cinétique est l'équivalent du produit d'un vecteur rotation par la masse et l'éloignement de l'objet qui tourne :
Figure 5.1 : exemple de rotation
Sur l'exemple ci-dessus, le moment cinétique d'une petite masse m qui irait de P à P' en tournant autour de O, sur le cercle de rayon R = OP = OP' serait le produit vectoriel :
(5.1)
Tout d'abord,
et
sont
tous deux
horizontaux et orthogonaux, donc
est
vertical
et donc colinéaire avec
.
En fait,
il est même toujours dirigé dans le même sens car
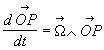, donc
,
et
forment un
trièdre
direct.
Or,
est
égal (en
module) au produit de la vitesse de rotation angulaire
ω par le vecteur
lui-même, c'est à dire ω .R. Le
module du vecteur
,
ou moment
cinétique est donc égal à
m.ω .R².
en fait,
=
m
R²
Le moment cinétique est dit "propre" quand il est calculé par rapport à un axe de l'objet lui-même (comme la Terre par rapport à son axe des pôles). Pour un objet volumineux qui tourne sur lui-même, il faut donc faire la somme (l'intégrale) de tous les moments cinétiques des parties infinitésimales qui le composent pour obtenir le moment cinétique propre total de l'objet.
Le spin correspond à un moment cinétique propre.
Le spin est quantifié et toujours multiple ou demi-multiple de la valeur h/2π (h est une constante appelée constante de Planck). Il peut par ailleurs être positif ou négatif (comme tout moment cinétique, sa valeur dépend de l'axe par rapport auquel on le mesure, et son signe de l'orientation de cet axe).
Dans l'étude des processus physiques, on a depuis toujours essayé de voir comment tel ou tel phénomène réagissait à certaines transformations. Par exemple, comment la vitesse et la position d'un mobile pouvaient varier suivant le référentiel dans lequel elles étaient mesurées (transformations de Galilée).
Toutes les transformations applicables aux événements physiques peuvent être regroupées en deux catégories :
a) les transformations d'espace-temps (rotation, réflexions) qui affectent finalement le repère dans lequel sont effectuées les mesures ou le système mesuré lui-même ;
b) les transformations internes au système étudié qui modifient réellement ce dernier (par exemple le remplacement des charges électriques par leurs opposées).
Une recherche corollaire a été de trouver des transformations par lesquelles l'image de l'univers (dans son entier) reste identique à l'univers lui-même. Le terme "identique" ne signifie pas "égal" : il veut simplement dire que les mêmes phénomènes physiques se produiront dans l'univers et dans son image, et que la description exhaustive de tout ce qui peut se produire dans ces deux univers ne permettra pas de différencier l'un de l'autre. En particulier, dans le domaine de la physique des particules, toute particule existant dans l'univers doit aussi se retrouver dans l'image et réciproquement.
On appelle une telle transformation une symétrie d'espace-temps.
L'exemple le plus facile est la translation d'espace : si l'on déplaçait tout l'univers de un mètre dans une certaine direction (encore faudrait-il avoir une référence externe à l'univers !), aucune loi de la physique n'en serait perturbée, les mêmes phénomènes microscopiques et macroscopiques se produiraient (bien sûr, dans ce cas, l'image est réellement égale à l'univers du départ, hormis les positions déplacées). Dans la réalité, ce n'est pas l'univers qu'on déplace mais le point à partir duquel on mesure certaines choses, et le fait est que cela n'a aucune incidence sur la nature de ce qui est observé. C'est donc une symétrie d'espace-temps.
Il y a en particulier trois transformations importantes qui reviennent souvent dans les considérations sur l'Univers ; elles sont désignées par les lettres C, P et T :
|
Lettre |
Intitulé | signification |
|
C |
Conjugaison de charge | transforme une particule en son antiparticule |
|
P |
Conjugaison de Parité | inverse le signe d'un axe spatial (réflexion-miroir) [9] |
|
T |
Inversion Temporelle | inverse le sens d'évolution des systèmes dans leur suite d'états |
Il existe un théorème (ou principe?), dit CPT selon lequel l'univers est invariant (au sens indiqué ci-dessus) par rapport à l'application de ces 3 transformations simultanées.
La symétrie CPT a toujours été observée. Elle implique entre autres que la masse et la durée de vie d'une particule sont exactement celles de son antiparticule, fait toujours vérifié. La violation de CPT aurait des conséquences énormes à la fois sur la physique des particules et sur la relativité générale. Selon les propres mots d'Abraham Païs (rapportés par Martin Gardner [Réf.2]), "Ce serait l'enfer".
On pensait autrefois que l'univers était également invariant vis à vis de chacune des transformations C, P et T appliquées séparément, mais en fait ce n'est pas le cas. Cela dit, ces violations sont relativement peu nombreuses et bien identifiées. Nous allons voir au paragraphe suivant ce qu'il en est de la parité.
P inverse le signe d'un axe de référence, ou de 3 (mais pas de deux, sinon c'est une symétrie par rapport à un axe, c'est à dire aussi une rotation de 180° par rapport à cet axe). Elle correspond à la symétrie par rapport à un miroir et inverse donc la droite et la gauche.
Pour un systèmes en rotation, P inverse le
sens de cette rotation
et transforme donc tout moment cinétique
en son
opposé
.
Elle inverse aussi les spins, les moments magnétiques, et donc la polarité des aimants (car elle correspond à une orientation du spin des atomes).
« Violation de la parité » est une expression équivalente à : « la transformation P n'est pas une symétrie ». Cela signifie que toutes les lois physiques ne sont pas conservées si l'on change le signe d'un (ou de 3) axe(s) de mesure de l'univers. Plus concrètement, cela veut encore dire que si l'on regarde l'image de l'univers dans un miroir, on y verra des phénomènes qui n'existent pas dans l'univers lui-même. Cela signifie que la séparation des notions de droite et de gauche est moins arbitraire qu'on ne le pense de prime abord.
Pourtant, jusqu'au 20 ème siècle, et même jusqu'en 1957, tout le monde, et ceci comprenait les physiciens (peut-être à une poignée de personnes près), pensait que tous les phénomènes physiques observables étaient symétriques (au sens gauche-droite).
En fait, c'est vrai de pratiquement tous les processus en oeuvre dans le monde. Même la déviation d'une aiguille aimantée par un champ magnétique émis par un courant électrique est un phénomène qui respecte la symétrie droite-gauche. En effet, son image dans le miroir n'inverse pas le courant, et donc pas le champ magnétique, mais elle inverse le spin des atomes de l'aiguille, et donc l'aimantation de celle-ci (c'est à dire les pôles nord et sud). C'est donc normal que l'aiguille tourne alors dans l'autre sens. C'est à dire que l'image dans le miroir n'est pas équivalente à l'original, mais que c'est un autre phénomène observable dans la nature.
Dans les années 50, la question de la conservation de la parité (c'est à dire du caractère symétrique de la conjugaison de parité P) fut soulevée lorsqu'on se heurta au problème des mésons K Thêta et Tau. Ces deux particules semblaient n'en être qu'une seule et même, sauf que l'une se décomposait en deux mésons pi alors que l'autre se décomposait en trois mésons pi. Or, pour des questions que je ne développerai pas ici, une particule unique susceptible de provoquer les deux types de désintégration violerait la parité. Comme il était impossible de trancher la question en observant les mésons K, la polémique sur le sujet en resta aux seuls discours.
Cependant, dans un article paru en 1956 [Réf.4], deux scientifiques américains, Chen Ning Yang et Tsung Dao Lee, décrivirent des expériences susceptibles d'apporter une preuve que l'interaction faible pouvait adopter des comportements non symétriques par rapport à la parité.
Une telle expérience fut réalisée en 1957 par l'équipe de Mme Chien Sung Wu [Réf.5]. Elle consistait à étudier la désintégration béta d'atomes de Cobalt (en atomes de Nickel), plongés dans un champ magnétique et à une température avoisinant le zéro absolu.
(7.1)
Dans ces conditions, les atomes de Cobalt s'alignent dans la direction du champ (ils sont polarisés). La confirmation de cette polarisation est effectuée par une mesure de rayons gamma émis lorsque l'atome de Nickel résultant de la désintégration béta du cobalt retourne à son état d'énergie minimum.
Figure 7.1 : atome de Cobalt aligné sur le champ magnétique
L'objectif de l'expérience était de regarder dans quelle direction s'échappaient les électrons émis par les noyaux durant la désintégration. Étant donnée la polarisation des atomes, toute particule chargée (et donc un électron) aurait tendance à en sortir par l'un des pôles (nord ou sud), mais a priori, il n'y avait aucune raison que ce fût l'un plutôt que l'autre. La statistique voulait donc qu'il sortît autant d'électrons par le haut que par le bas.
Cependant, les mesures montrèrent que les électrons sortaient préférentiellement par le bas du dispositif. Le rapport exact était de 60% contre 40. Lorsqu'on laissait le système se réchauffer, cette prédominance diminuait, puis disparaissait au bout de 6 minutes, parce qu'à ce moment, l'alignement des atomes de cobalt n'était plus systématiquement dans le sens du champ magnétique imposé.
En fait, cela voulait dire que les électrons ne sortaient pas préférentiellement par le pôle sud des atomes de cobalt, mais qu'ils sortaient toujours par ce pôle, et qu'on ne pouvait mettre ce résultat en lumière que lorsqu'on était sûr de connaître l'alignement majoritaire des atomes de Cobalt au départ. Si le rapport n'avait pas été de 100 contre 0, c'est parce que seulement 60% des atomes de Cobalt s'étaient bien alignés (à cause des conditions de l'expérience) et pas parce qu'un électron donné ne sortait par le pôle sud de l'atome que dans 60% des cas.
En tout cas, cela violait la parité parce que l'image de ce processus dans un miroir eût été des atomes de Cobalt orientés de polarité inverse (car celle-ci correspond à une rotation propre), mais des électrons s'échappant toujours par le bas, donc cette fois par le pôle nord (voir figure 7.2), phénomène impossible comme cette expérience l'avait prouvé.
Figure 7.2 : La désintégration béta du Cobalt 60, et son image hypothétique dans le miroir
Dans les mois qui ont suivi l'expérience de Mme Wu, on s'est demandé ce qui pouvait sous-tendre l'asymétrie observée. Rien dans le comportement habituel des électrons ne pouvait l'expliquer. En revanche, on ne connaissait pas totalement le comportement des neutrinos. Le résultat de l'expérience pouvait se comprendre si les neutrinos produits étaient d'hélicité gauche (et inversement les antineutrinos d'hélicité droite).
Jusqu'alors on n'avait jamais rencontré aucune particule qui manifestât une tendance particulière pour une hélicité ou l'autre. Ceci était d'ailleurs impossible pour une particule massive car celle-ci avait alors une vitesse inférieure à celle de la lumière (conséquence dictée par la théorie de la relativité restreinte), et il suffit alors de la rattraper et d'aller plus vite qu'elle pour inverser sa vitesse, mais pas son sens de rotation, ce qui inverse aussi l'hélicité.
<< L'hélicité d'une particule massive est dépendante du repère de mesure. >>
En revanche, une particule de masse nulle (comme on soupçonnait que le neutrino le fût) une fois produite garde la même hélicité. Mais pourquoi une telle particule serait-elle toujours produite avec la même hélicité ?
Pour en avoir le coeur net, une expérience de mesure de l'hélicité des neutrinos fut montée en 1958 par Maurice Goldhaber [Ref.6]. Elle consistait à mesurer l'hélicité du neutrino produit dans la réaction suivante :
(7.2)
L'électron capturé par le noyau d'Europium est l'un de ses propres électrons, de la couche K. Le Samarium résultant est dans un état excité. En retombant dans son état fondamental, il émet un rayonnement γ. Or, le noyau de Samarium excité a la même hélicité que le neutrino, et son temps de vie étant très court, transmet la même polarisation aux rayons γ qui sont émis dans la direction opposée à celle du neutrino. La polarisation de ces rayons est déterminée en examinant leur passage à travers du fer magnétisé (qui jour le rôle d'un filtre polarisant).
Le résultat a été que tous les neutrinos produits étaient d'hélicité gauche.
Dans toutes les mesures faites jusqu'à présent, on n'a pas pu mettre en évidence le fait que le neutrino était massif ou non. Ce que l'on sait, en revanche, c'est que cette masse si elle n'est pas nulle, est inférieure à 35 eV/c 2 (soit : 1,78267 10 -36 kg).
Néanmoins, le fait que le neutrino ait une masse intéresse certains physiciens, car il pourrait expliquer deux phénomènes :
1) la « masse manquante » de l'univers :
Les mesures sur la quantité de matière dans l'espace intersidéral, voire intergalactique montrent que sa densité globale et locale est trop faible pour :
1a - équilibrer l'expansion de l'univers à long terme. Ceci n'est pas une contradiction en soi, mais détruit une certaine harmonie dans l'image de l'univers.
1b- empêcher les galaxies de se disloquer sous l'effet de la force centrifuge consécutive à leur rotation.
Les neutrinos sont si nombreux que leur masse hypothétique, même minime individuellement, fournirait sans doute la fameuse masse manquante. Mais diverses théories en cours d'élaboration proposent des explications alternatives (matière sombre, interactions contra-gravitationnelles entre régions de l'univers « conjuguées »...).
2) l'oscillation neutrinique :
En fait, il existe 3 types différents de neutrinos, associés chacun à un type de particule massive de même famille que l'électron, l'ensemble des 6 appartenant à ce qu'on appelle les leptons. Les leptons les plus lourds [10] comprennent dans l'ordre croissant de leur masse : électron, muon et tauon (e, μ et τ ), tandis que les « légers » sont les neutrinos. Associés chacun à un lepton massif, ils s'appellent respectivement neutrino électronique, muonique et tauonique (νe, νμ et ντ).
Jusqu'à présent on n'a vu que le couple e-νe dans la réaction (1.4), mais il existe pour chaque paire lepton lourd/neutrino associé le même type d'interaction (faible).
Le soleil produit beaucoup de neutrinos électroniques par la réaction suivante, par laquelle deux protons forment un noyau d'hydrogène (deutérium) :
(8.1)
Or, si l'on essaie d'intercepter ces neutrinos lorsqu'ils arrivent sur terre, on en trouve de deux à trois fois moins que prévu. L'explication avancée est qu'il existe une oscillation inter-neutrinos, c'est à dire que tout neutrino au cours du temps peut se transformer spontanément en l'un des autres types de neutrino (les méthodes d'interception ne mettant en évidence que les neutrinos électroniques).
Cette théorie se traduit par le fait que les 3 neutrinos seraient en fait 3 états observables d'une seule et même particule (LE neutrino « générique »), hypothèse qui peut se formaliser en mécanique quantique avec le calcul du passage d'un état à l'autre (voir [Ref.1, pp 626-627] et [Ref.7, pp.178-179]).
Mais pour cela, il faut supposer que :
1 - les neutrinos n'aient pas tous la même masse (ce qui sous-entend que seul l'un au maximum peut avoir une masse nulle)
2 - les états observables pour l'interaction faible (νe, νμ et ντ) ne soient pas les états propres de la mesure liée à la masse du neutrino (sinon, une fois dans un état, ils n'en bougeraient plus). Ce seraient en fait des états de superposition.
Si l'on se ramène à seulement deux états de neutrinos a et b pour l'interaction faible, il existerait une base de vecteurs propres, disons |ν 1> et |ν 2> pour la mesure de masse.
On aurait alors |a> = a1 |ν
1> + a2 |ν 2>
et
|b> = b1 |ν 1> + b2
|ν 2>. En fait, |a> et
|b>
seraient eux-mêmes à la fois normés (vrai de tout
vecteur
d'état) et orthogonaux, d'où on peut trouver un nombre
θ
(appelé angle de mélange) tel que a1 = b2 =
cos(θ)
et a2 = -b1 =
sin(θ).
D'où : |a> = cos(θ) |ν 1> + sin(θ) |ν 2> et |b> = -sin(θ) |ν 1> + cos(θ) |ν 2>
A un moment donné, le neutrino « générique » est dans un état y qui est une superposition des deux états |ν 1> et |ν 2>. Le vecteur/fonction d'onde associé est :
|y > = <α |a> + β |b> avec <α 2 + β 2 = 1 (8.2)
Si au départ (émission par le soleil), le neutrino est dans l'état disons a, alors
|y o> = |a>= cos(θ) |ν 1> + sin(θ) |ν 2> (8.3)
On peut calculer l'évolution du vecteur/fonction d'onde dans le temps, suivant une loi énoncée par la mécanique quantique :
|y
(x,t)>
=
cos(θ)
|ν 1>
exp(i
)
+
sin(θ)
|ν 2>
(i
)
(8.4)
où
est la constante de Planck h
divisée par
2π.
On voit alors sans discussion possible que si les deux masses sont nulles, il ne peut y voir d'évolution car alors E = pc, d'où Et = pct = px, et l'exposant de chaque exponentielle est nul.
Pour qu'il puisse y avoir oscillation neutrinique, il est nécessaire que l'un des neutrinos ait une masse non nulle. En fait, vue l'analogie des relations des 3 couples de leptons lourds/neutrinos, si l'un des neutrinos est massif, ils le sont nécessairement tous les 3. De plus, on a aussi mis en évidence le fait que les neutrinos muoniques avaient eux aussi une hélicité fixe gauche.
Elle tient en une phrase : « la violation de la parité dans l'interaction faible repose sur le fait que le neutrino (électronique, muonique) a une hélicité constante (gauche), or si le dit neutrino a une masse, alors il ne va pas à la vitesse de la lumière et son hélicité change selon que l'on va plus ou moins vite que lui ».
Si l'on résume toutes les étapes :
Une violation de la parité a été mise en évidence lors d'une expérience basée sur l'éjection d'électrons d'un noyau de cobalt. Elle se traduit aussi par le fait que les neutrinos électroniques n'existent que dans l'état d'hélicité gauche, c'est à dire que la mesure de la projection de leur spin suivant la direction de leur vecteur vitesse est toujours négative, tandis que l'antineutrino, lui, est toujours d'hélicité droite (vérifié aussi pour les autres neutrinos). Cette caractéristique est dépendante du fait que le neutrino se déplace à la vitesse de la lumière et qu'il est donc impossible d'aller "plus vite" que lui (sinon, dans un référentiel plus rapide, son vecteur vitesse serait inversé et donc le signe de la projection du spin aussi).
Pourtant, l'on soupçonne le neutrino de ne pas être de masse nulle, auquel cas l'ensemble des neutrinos de l'univers pourrait même en constituer ce qu'on appelle la "Masse Manquante". C'est de plus la seule explication valable pour le manque de neutrinos électroniques détectés sur terre.
Pourtant, un neutrino massif ne pourrait pas aller à la vitesse de la lumière (même s'il en était très proche) et ne conserverait donc pas une hélicité constante selon le référentiel (plus rapide que lui ou moins rapide) dans lequel la projection de son spin sur son vecteur vitesse serait mesurée.
Donc, la supposition d'une masse non nulle du neutrino explique l'oscillation mais est incompatible avec la violation de la parité dans l'interaction faible.
Réf.1 "Nuclear and Particle Physics" par W.E. Burcham et M. Jobes (Longman Scientific & Technical, 1995)
Réf.2 "L'Univers ambidextre" par Martin Gardner, traduction française (collection Science Ouverte, Editions du Seuil, septembre 1985)
Réf.3 "La Physique des particules élémentaires de sa naissance à sa maturité 1930-1960" par Jeanne Laberrigue-Frolow (Editions Masson, Paris, 1990)
Réf.4 « La question de la conservation de la parité dans l'interaction faible », par T. D. Lee & C. N. Yang, 1956, Physical Review, 104 (254)
Réf.5 « Experimental Test of Parity Conservation in Beta Decay », par C.S. Wu, E. Ambler, R.W. Hayward, D.D. Hoppes and R.P. Hudson, 1957, Physical Review, 105, 1413-1414(L)
Réf.6 M. Goldhaber, L. Grodzins & A. W. Sunyar, 1958, Physical Review, 109 (1015)
Réf.7 "Cours de Physique - Mécanique Quantique", Tomes I et II, par J.L. Basdevant (Ecole Polytechnique, 1983)
Figure 2.1 Spectre d'impulsion du rayonnement Béta
Figure 3.1 : repère Oxyz
Figure 3.2 : les 2 orientations de l'espace
Figure 4.1 : sphère en rotation
Figure 4.2 : rotations droite et gauche
Figure 4.3 : une rotation droite de 90° fait passer de Ox à Oy
Figure 4.4 : effet des réflexions-miroir sur le sens des rotations
Figure 4.5 : hélicités droite et gauche
Figure 4.6 : hélices droite et gauche
Figure 4.7 : exemple du tire-bouchon d'hélicité droite
Figure 4.8 : vecteurs rotation
Figure 4.9 : vecteurs rotation et vitesse
Figure 5.1 : exemple de rotation
Figure 7.1 : atome de Cobalt aligné sur le champ magnétique
Figure 7.2 : La désintégration béta du Cobalt 60, et son image hypothétique dans le miroir
Rappel : On sait qu'en mécanique quantique, l'état d'un système d'une manière générale est une fonction d'onde y à laquelle on fait correspondre un vecteur |y > normé d'un espace complexe de Hilbert. Les états observables ou mesurables d'un système sont les valeurs propres d'un opérateur hermitien appelé observable. A toute opération de mesure correspond donc une observable qu'il faut "tailler sur mesure" (l'espace de Hilbert aussi d'ailleurs). Par exemple, les valeurs possibles de l'énergie d'un système sont les valeurs propres de l'opérateur H appelé aussi Hamiltonien. Une valeur propre d'un opérateur A est un nombre <α pour lequel il existe un vecteur |a> tel que : A |a> = <α |a>. |a> est alors appelé un "état propre" de l'opérateur A, pour la valeur propre <α .
Dans la pratique, pour un opérateur donné, on cherche à trouver une base de l'espace de Hilbert composée uniquement d'états propres |ei>. Chacun d'entre eux vérifie A |ei> = <α i |ei>. Dans ce repère, la matrice de A est diagonale et les <α i correspondent aux nombres sur la diagonale.
Si le système est dans l'état y , le vecteur associé |y > se décompose dans la base des |ei>, sous la forme:
Dans ce cas, |θ i|2 est la probabilité que la mesure correspondant à A donne la valeur <α i. L'état du système avant mesure est y (ou |y >, cela revient au même). Après la mesure, il est dans l'état |ei>,correspondant à la valeur propre trouvée <α i. Il est "stabilisé".
[Note 1] appelés parfois pour cette raison particules b. L'électron - en tant que particule - a été découvert en 1896 par J.J. Thomson (Prix Nobel 1906).
[Note 2] on sait qu'il existe 4 interactions (ou forces) fondamentales : la gravitation, l'élecromagnétisme, et les deux forces nucléaires (faible et forte). On considère de plus en plus qu'elles sont toutes 4 issues d'une même et unique force primordiale, leurs aspects différents actuels s'expliquant "historiquement" par des phénomènes de "brisures de symétrie" survenus dans les tous premiers instants de l'univers.
[Note 3] qui a découvert le neutron en 1932 et a obtenu pour cela le Prix Nobel de physique en 1935.
[Note 4] le schéma détaillé de l'interaction forte fait intervenir les sous-composants des nucléons (les quarks) ainsi que des "messagers" d'interaction appelés gluons. Par ailleurs, toutes les particules sensibles à l'interaction forte (car les neutrons et les protons sont loin d'être les seules) sont appelées hadrons.
[Note 5] particule d'antimatière "conjuguée" avec le neutrino. Les deux particules, si elles sont mises en présence, s'annihilent réciproquement
[Note 6] le positron (ou positon) est une particule d'antimatière "conjuguée" avec l'électron dont elle possède toutes les caractéristiques connues, sauf la charge électrique qui est exactement l'opposé. Les deux particules, si elles sont mises en présence, s'annihilent réciproquement (avec production de rayonnement γ ). Le positron est la première particule d'antimatière qui a été découverte (en 1931 par Carl Anderson).
[Note 7] En effet, tout ici est une question de quantité, car la réaction 1.5 peut théoriquement avoir lieu n'importe où étant donné l'abondance d'antineutrinos dans l'univers. Mais, vu leur faible interaction avec les autres particules, il faut vraiment une densité importante d'antineutrinos à un endroit donné pour avoir une chance d'observer cette réaction.
[Note 8] Sur notre schéma, nous avons amplifié le déplacement (il est loin d'être infinitésimal), mais en définitive, ce qui compte est le fait que le point est toujours resté du même côté de l'axe.
[Note 9] Certains [Réf. 1] ajoutent ensuite une rotation de 180°. Cette opération supplémentaire ne change pas intrinsèquement l'état du système, mais peut amener des confusions si l'on regarde quelle quantité l'opération P conserve (spin, moment...)
[Note 10] expression presque antinomique car « lepton » signifie « léger » !